A Network Is Always A Tradeoff
The Important
Version: 3, 1:06 PM PDT, September 15, 2020
The very act of building a network with routers and switches is a decision to make tradeoffs.
As topologies approach structures that are economically, technologically, and aesthetically challenging, they will tend towards new topology/networking that addresses those challenges. Failure to do so will likely inhibit growth.
Aesthetically unpleasing topologies will likely change, because they may also be hard to understand, and therefore operationally complex, all things being equal, for example approaches to tools and management.
There are often tradeoffs between network complexity and operational complexity.
Tradeoffs are often between the cost of adding a capability and the cost/consequence of not adding a capability, for a given topology and given capacity.
Some tradeoffs may be mitigated by changing topology and/or adding capacity.
Complexity often comes with the need to make choices.
Choice itself an additional complexity.
A network designer’s role extends beyond the network itself, and deeply into operations. An additional and/or alternative observation is that operations tools and methods may expand topology optionality.
Choices can shift profit from one profit pool to another.
In “Why We Build Networks” there was discussion on the evolution from point to point links to a network structure, because point to point is not economically, technologically, or aesthetically scalable. This discussion was in the context of connecting billions of smart phones with point to point links - something we clearly accept as being not feasible.
This article revisits that premise, using mathematics networking professionals are already familiar with, while also illuminating another point made in “Why We Build Networks”
“The very act of building a network with routers and switches is a decision to make tradeoffs.”
In this article, the term “switch” is used generically to refer to the process of deciding which link information should be forwarded on. The term is not specific to either Ethernet switching or IP routing.
The n-1 and n (n-1) / 2 problem
As diagrams a,b,c, & d in figure 1 show, if we choose to have a point to point link (edge) between every node (vertex), then every time we add a new node, we have to add n-1 links resulting in a total of n (n-1) / 2 links.

Figure 1. The n-1 and n (n -1) / 2 problem
As figure 1 also shows, there is one or more alternatives, example diagram E, and of course derivatives with additional redundancy. E has 5 links compared to 10 links in D.
E is a technologically viable alternative if the switching capacity is equal to the sum of all links or the sum of all busy hour loads on each link; perhaps even the sum of all peak loads. If the switching capacity is not, then more complexity/cost may be needed in the switch to support queuing, priority-based switching, and other QoS mechanisms; accompanying that complexity will be additional complexity in the form of making choices/tradeoffs. Additional switching capacity could also be constructed.
E is an economically viable alternative if it is a) technologically feasible, and b) less expensive than D. Less expensive has many nuances of course. Less expensive from the perspective of operations and/or less expensive from the perspective of whoever owns the capital budget.
E is aesthetically viable if it brings more pleasure to observe and/or it improves understanding. The latter is an interesting issue. Is something less complex just because it is easier to understand? Here again there may be nuance. A point-to-point meshed topology may not be more complex from the perspective of many aspects of the system: everyone has guaranteed access to a channel without complex QoS, arguably there is greater privacy, there is no chance of information being switched to the wrong destination, by the topology itself, without the need for extra error-checking complexity. In many ways it is less complex. However, if a human cannot visualize it, or workout what the connectivity is, is it more or less complex? It may be less complex from an equipment perspective, and more complex from an operations perspective - in this speculation is a realization that a network designer’s role extends beyond the network itself, and deeply into operations; something to be touched on in future articles. An additional and/or alternative observation is that operations tools and methods may expand topology optionality.
A Network of Switches
Now extend the small switched network to a network of switches and the result is 31 links vs the 190 that would be required for a point to point topology of 20 nodes: 20x(20-1) / 2.
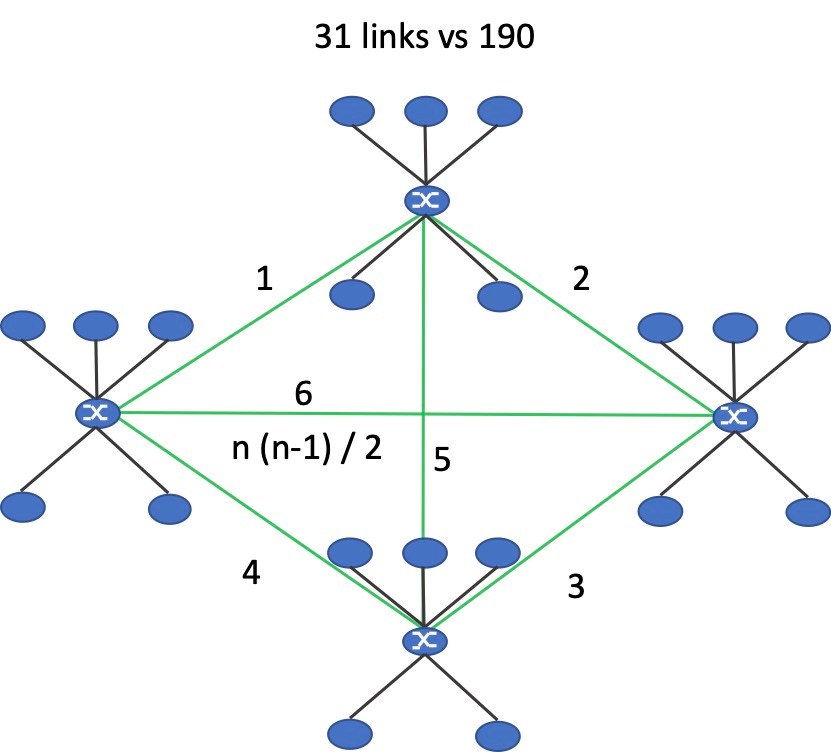
Figure 2. A network of switches
Once again if the switching capacity and the inter-switch link capacity is sufficient to carry peak loads, then this approach is technologically feasible. If not, then more complexity needs to be added in the form of QoS, and choices have to be made. Maybe more switching capacity could be added as well.
Perhaps the more stunning observation, at scale, is how many links are eliminated. Hence, the value of the switch, is the cost of the no longer needed links, minus some additional switch and management cost - in other words it is an arbitrage which may over time settle at whatever profit suppliers are willing to take for delivering a switch. Anyone lose in this equation? Anyone involved in developing and selling links did. It is a shift of value / profit from one profit pool to another, providing the incentive for entrepreneurs to develop switches.
More tradeoffs
Should the switching equipment support a way to select the best option among the many paths between the different switches? This would add more cost & complexity.
Should the switching equipment support a way to spread the load over all links? This would add more cost and complexity.
Should the switching equipment support virtual topologies, one for each different class of traffic? That would add more cost and complexity.
Should the topology have more redundancy? That would add more cost and complexity.
Tradeoffs are often between the cost of adding a capability and the cost/consequence of not adding a capability, for a given topology and given capacity. Some tradeoffs may be mitigated by changing topology and/or adding capacity.
Conclusion
This article takes it as self-evident that if a topology becomes economically or technologically unfeasible, it will not long endure, it will evolve to a new topology that addresses the economic and technological challenges. Changes will likely involve tradeoffs and choices. Alternatively, if not addressed, the lack of economic and technological viability will lead to lack of growth.
This article does not take it as self-evident that topologies that are aesthetically unpleasing, will evolve to topologies that are pleasing, human behavior being full of nuance and lack of predictability. However, this article does assert a speculation that aesthetically unpleasing topologies will likely change because they may also be hard to understand, and therefore operationally complex, all things being equal, for example approaches to tools and management. This article does not assert that aesthetically pleasing topologies will have better availability, more optimal routing, or any similar characteristics.

