Axioms - Information

WORK IN PROGRESS (WIP) Revision 0.4 December 10, 2022

In classical systems

Axioms

Summary

1. Information is Relative

2. No information function is omniscient

3. No information function is omnipotent

4. Necessary information increases certainty

5. Information cannot be reduced below what is necessary

6. Complexity cannot be reduced below what is necessary

7. Equivalent functions cannot be reduced below necessary information

8. Equivalent functions cannot be reduced below necessary complexity

9. Information is (in)sufficient

10. Information is (un)clear

11. Information is (in)accurate

12. Necessary information is sufficient, clear, accurate

13. Summarization reduces information

14. Summarization reduces certainty

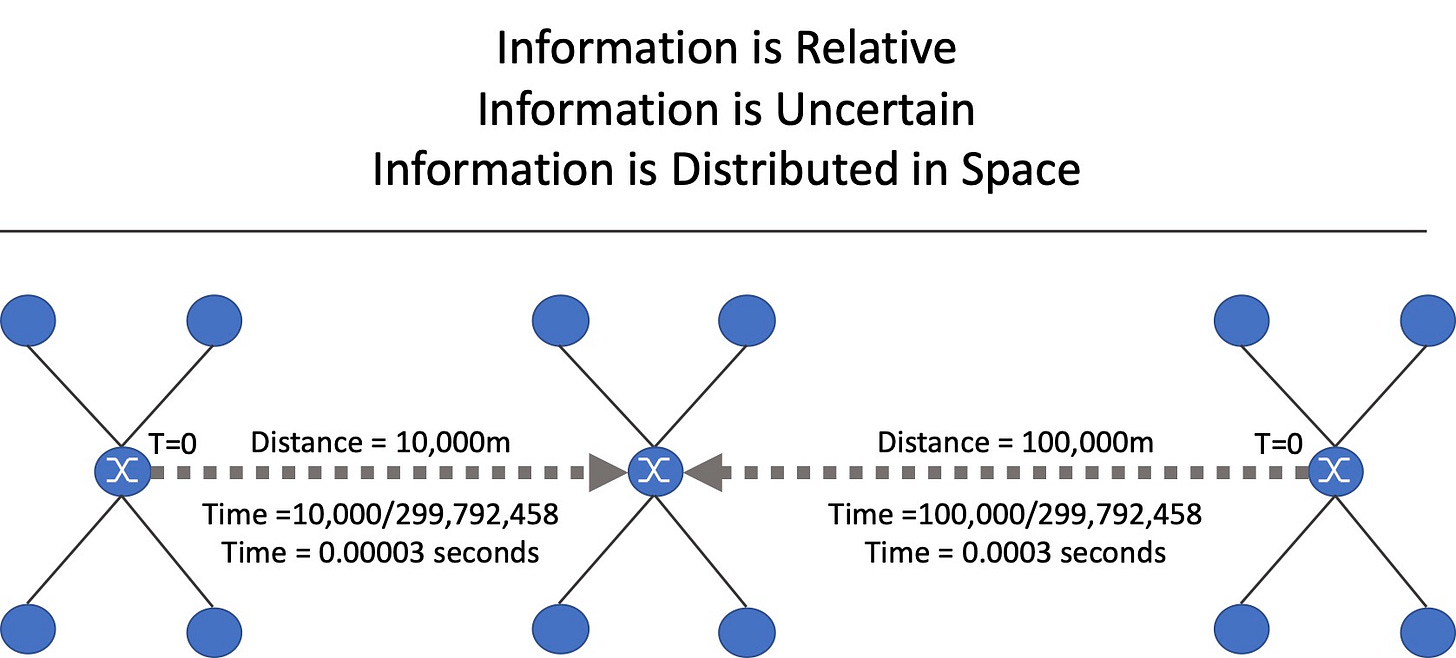
Figure 1. Information is Relative, Uncertain, and Distributed in Space

A1. Information is Relative

1. Information resources are distributed in space

2. Movement of information resources has a finite speed

3. Movement of information resources takes time

4. Information is relative to where an information function is in space

5. Different observers, separated in space, will disagree on when an event occurred and the sequence of events.

A2. No information function is omniscient

1. Information is relative to were an information function is in space

2. No information function has instantaneous access to all information

3. No information function is omniscient (all knowing)

A3. No information function is omnipotent

1. Information resources are distributed in space

2. No information function has access to all resources at any given point of time

3. No information function is omnipotent (all powerful / infinite resources)

A4. NECESSARY Information increases certainty

1. A + B = C

2. If A and B are known, the value of C is certain

3. A and B increase certainty

4. If A and Z are known, but B is not known, then C is also not known.

5. A and Z do not increase certainty.

6. Necessary information increases certainty.

A5. Information cannot be reduced below what is necessary

1. A + B = C

2. The value of C is not certain unless A and B are known

3. A and B is the necessary information to be certain of the value of C

4. For a given function, equation, etc information cannot be reduced below what is necessary

A6. Complexity cannot be reduced below what is necessary

1. A + B = C

2. The value of C is not certain unless A is added to B

3. Adding A and B is necessary complexity

4. For a given function, equation, etc complexity cannot be reduced below what is necessary

A7. Equivalent functions cannot be reduced below necessary information

1. A + B = C

2. G + H = C

3. A=2, H=2

4. Therefore, G = B

5. Superficially the equations look different

6. Substantively the equations are the same, differing only by how information was labelled

7. Equivalent functions cannot be reduced below necessary information

A8. Equivalent functions cannot be reduced below necessary complexity

1. A + B = C

2. G + H = C

3. A=2, H=2

4. G=2, B=2

5. Superficially the equations look different

6. Substantively the equations are the same, differing only by how information was labelled

7. Both equations add two numbers to derive a third (C)

8. Equivalent functions cannot be reduced below necessary complexity

A9. Information is (in)sufficient

1. A + B = C

2. The value of C is not certain unless information is sufficient (A,B)

3. At the moment the equation ‘A + B = C’ is computed, the available information is either sufficient (A,B) or insufficient (A or B but not both)

A10. Information is (un)clear

1. A + B = C

2. The value of C is not certain unless information is clear (A,B)

3. At the moment the equation ‘A + B = C’ is computed, the available information is either clear (A,B) , impacted by noise (A,Z), or impacted by redundancy (A,A,A,B,B,B)

4. Information is clear or unclear

A11. Information is (in)accurate

1. A (2) + B (2) = C (4)

2. The value of C is not accurate unless information is accurate (2,2)

3. Information is either accurate or inaccurate

A12. Necessary information is sufficient, clear, accurate

1. A bowl as two apples and three oranges in it

2. The quantity of fruit is computed by the function A + O = F

3. Information available for equation (2,3)

4. Information available is sufficient (both A & O)

5. Information available is clear (not having noise or redundancy)

6. Information available is accurate (the correct quantities for A & O)

7. Quantity of fruit is computed as 2+3=5

8. Quantity of fruit is accurate

9. Necessary information is sufficient, clear, and accurate

A13. Summarization reduces information

1. {2,2,2,2,2,2,2,2,2,52}

2. Average = 7

3. The information that most values were 2 was lost

4. Summarization reduces information

A14. Summarization reduces certainty

1. Information increases certainty

2. Summarization reduces information

3. Summarization reduces certainty

Appendix A - Definitions of Information

1. The unit of information is a bit

2. A bit has one value only, either zero or one

3. Information storage, processing, and propagation obey the laws of physics

4. The maximum speed of information is the speed of light

5. The minimum propagation delay of information is ( distance / speed of light )

Appendix B - Equations and Values

1. The speed of light is a vacuum is, 299,792,458 meters per second

2. The number of links in a complete graph is equal to: n (n-1) / 2

3. Time = distance / velocity

Appendix C - Time

1. Time is how long it takes light to travel a measured distance

2. Measured time changes, if measured distance changes, relative to observation

3. Time and sequence of events is relative to the frame of reference

Appendix D - Existing Axioms

Pre-existing axioms already established in other disciplines that may also be relevant to discussions of Information / information networks.

Euclid: “Things equal to the same thing are equal to each other.”

1. Mathematics Reflexive Axiom: Information is equal to itself.

2. Mathematics Symmetric Axiom: If a = b then b = a.

3. Mathematics Transitive Axiom: If a = b and b = c then a = c.

Euclid: “A point is that which has no part”

• A point is a specific location in space. Points describe a position, but have no size or shape themselves.

Euclid: “A line is breadthless length”

• A line is a set of infinitely many points that extend forever in both directions. Lines are always straight and have no width.

Euclid: “The ends of a line are points”

• A line segment is the part of a line that lies between two points, without extending to infinity. We can label line segments from point A to point B as AB‾.