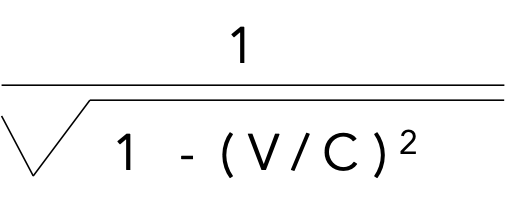Derivation of Equation for Time Differences Between Moving Clocks
With gratitude to all scientific thinkers
Thanksgiving Preface
In commemoration of Thanksgiving 2022, this derivation of the gamma (γ) equation / Lorenz Factor is provided as a gesture of gratitude for all the scientists that have made great contributions to the world we live in, providing a deeper understanding of it, with the imagination to go beyond what is conventional wisdom / intuitive from every day experiences. Some of these new ways of thinking are framed in mathematical language, and perhaps can only be fully understood by diving into the mathematics. Hence, this post.
May concepts such as time dilation continue to engages us and invoke our curiosity WRT the true nature / reality of life.
Introduction
Gamma (γ) / the Lorenz Factor is a famous equation that is used in many ways, including aspects of time dilation such as determining the ratio of the elapsed time of a stationary clock to the elapsed time of clock in relative motion. The equation returns a value over 1. Until the speed of the moving object approaches the speed of light, the value is not much above 1, which is consistent with the lack of attention time differences get in daily life - we don’t notice them. The equation for γ is:
Figure 1. “Gamma” equation / Lorenz factor
The purpose of this post is to derive the formula using a conceptual “photon” clock. This is based on the derivation provided in Special Relativity with Brian Greene,
. This post aims to provide a step-by-step, and hopefully simple explanation.
The fundamental ideas are not my own.
The use of a conceptual photon clock is not my own.
All words are intended to be my own.
All diagrams are intended to be my own.
All mistakes are most definitely my own.
Absolute Rest and Relative Motion
Recall, Einstein asserted that there is no absolute rest. All bodies are in motion. A person walking is in motion relative to the Earth, the Earth is in motion relative to the Sun, and so on. In this derivation, there is no attempt to incorporate the motion of bodies relative to all other bodies, only the relative motion between the two bodies.
Two Photon Clocks
Physicists claim that time will be measured differently by observers with different constant velocity, regardless of the mechanism for measuring time. As long as the mechanism is a repetitive, cyclical, periodic mechanism, the principle will apply. A conceptual photon clock is used because of its internal simplicity, and therefore the ease of describing the mechanism.
For most people, a photon clock is a thought experiment, you cannot order one online. Conceptually, it is a device with a top and bottom mirror. A single photon oscillates between the top and bottom with regular periodicity: tick, tock, tick, tock, tick, tock,…
Figure 2. Conceptual Photon Clock
Consider two photon clocks occupying the same space / location1. They have the same mechanism for measuring time and there is no speed difference relative to each other. Both clocks will express time in the same way.
Figure 3. Two Photon Clocks at the same location
Now we place Clock A in motion, relative to Clock B, at a constant velocity.
Figure 4. Clock A is placed into motion with constant velocity
Now that Clock A is in motion, an observer at Clock B would see both the mirrors of Clock A moving, and hence, the photon would now reflect at an angle to the mirrors, to keep striking them. This is no different than someone above the earth watching a boy bounce a ball on the ground. From that person’s perspective, the ball would move with the rotation of the earth, even though the boy would not perceive any rotation, as the boy’s own rotation would be the same as the ball.
Figure 5. An observer at Clock B would now perceive the photon in Clock A reflecting at an angle
Now that the distance travelled by the photon in Clock A is longer when observed from Clock B, the question becomes how does this impact time? More specifically, how does this impact Clock B’s perception of Clock A’s time, relative to Clock B’s own time.
Derivation Goal
Clock A is in motion relative to Clock B. We now wish to determine the length of a tick in Clock A, as seen by Clock B, relative to a tick as seen by Clock A. This will be referred to as La / Lb.
Figure 6. Goal is to determine relative elapsed times
However, we do not know either La or Lb, all we know is the speed of the photon, C, and the speed of Clock A, relative to Clock B, which we shall call “V”. Using C & V, as well as trigonometry, we will determine the ratio of time as observed by Clock B and Clock A.
Derivation
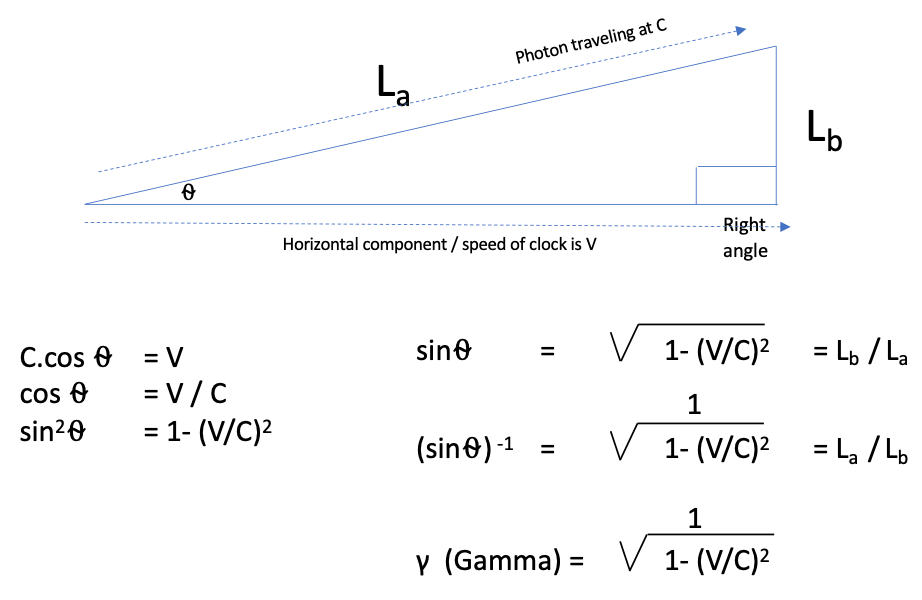
To do the derivation we will construct a right-angle triangle and apply trigonometry. We are looking for the ratio of La to Lb or La / Lb. As sin⍬ = opposite / hypotenuse or Lb / La, the inverse of what we are looking for, we need to derive an equation equal to inverse of that 1/(sin⍬).
Figure 7. Equivalent trigonometric function to the solution
What do we know? C = the speed of the photon; V = the speed of the clock in motion, Clock A. These velocities are associated with the adjacent and hypotenuse of angle ⍬, which is a cosine function. We start there, with what we have.
Figure 8. Deriving cos ⍬
C. cos ⍬ = V is the equation for the horizontal component of C. By intuition, the photon must be moving at the same horizontal velocity as Clock A, or it would not reflect off the mirrors in Clock A.
Therefore, the derivation can start with either:
C. cos ⍬ = V rearranged to cos ⍬ = V / C
Or simply by determining the cos of ⍬ which also equals V / C
[Apologies, the following steps are in the document as an image, because this editor does not yet support superscripts and subscripts]
The full derivation is shown in figure 9.
Figure 9. The full derivation of the equation.
Applying The Equation
The below table shows the values of γ for various values of V, the constant motion of Clock A. As can be seen, the speed of Clock A has to approach the speed of light before there is a significant difference between Clock A’s time and the time an observer at Clock B perceives Clock A’s time to be. This is why we are not aware of the difference in everyday life, because we are never comparing clocks with significant relative speed differences.
OTOH, the difference in perceived time becomes quite large as the speed of Clock A is almost equal to C.
Discussion
The construction of a triangle allows for a solution by pythagorean principles. However, the lengths of at least two sides are not known, so those principles cannot be directly applied. That said, the use of “sin2⍬ + cos2⍬ = 1” in the solution, leans on those principles.
It is important to note that from the perspective of each clock, its own photon is oscillating up and down without the angle used in this derivation. The angle exists only from the perspective of an observer at the “stationary” clock viewing the “moving” clock. Is this possible? The earth rotates at 1,000 miles per hour / 460 meters per second. An observer that was stationary with respect to this rotation would view this regularly, or at least view bodies moving from their original position relative to the observer.
Whether a clock is mechanical or atomic it is impacted by motion and gravity. Changes to motion and gravity impact the mechanism. Is this evidence that there is no such thing as absolute time in the way Newton thought of it, or simply that two clocks being impacted by different physical forces no longer measure time in the same way? That question, the author leaves as an exercise for the reader to ponder. What is clear though, is engineers need to account for these differences in real world applications, for example Global Positioning System (GPS).
The idea that there is no absolute rest or absolute time were significant departures from the then prevailing Newtonian mechanics. These departures occurred during a time when there was great scientific interest in the nature and equations of electromagnetism, which were revealing some new challenging questions.
Albert Einstein’s postulates that gave us a new way of thinking about the universe we live in, were included in a paper titled “ON THE ELECTRODYNAMICS OF MOVING BODIES” and started with the sentence (translated to English), “It is known that Maxwell's electrodynamics—as usually understood at the present time—when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena”.
When science explores a new aspect of the universe we live in, it sometimes challenges those things which we currently hold to be true.
Experimental Evidence for Time Dilation
For networking / communications professionals, the most often quoted example is the adjustment for time dilation in GPS. Note particularly, section 2.6 of the following document, where the equation in this post is explicitly mentioned: Global Positioning System Receivers and Relativity.
Other references:
Occupying the same space / location was stated as there have been recent experiments suggesting that atomic clocks even a few centimeters apart can show small differences.